I have just posted on arXiv yet another preprint about Newtonian semi-classical gravity. It is not really an improvement from previous work but rather an easy introduction to the idea and the concepts, using a mathematically simpler basis.

Let me recall how I understand the problem of semi-classical gravity. If a semi-classical theory of gravity is to be fundamental, it has to specify two things:

1. How quantum matter moves in a given classical curved space-time.
2. How quantum matter curves this classical space-time.

The first point is I think pretty standard. In the general relativistic context it is answered by quantum field theory in curved space time but in the Newtonian limit, being so fancy is not even necessary. To specify the influence of space-time on quantum matter, one just puts the gravitational field as an external field in the Schrödinger equation. The tricky part is the second aspect: how quantum matter back-reacts on space-time. This problem is basically open. In the Newtonian limit, it means finding a good candidate for the gravitating mass density.

To construct a (classical) mass density field from quantum matter, a tempting thing is to do is just to project down to real space some properties of the wave function (that lives in configuration space). This is the historical idea but this is a bad idea. Taking for example (where is the mass density operator) as a candidate for the mass density gives a gravitational field depending quadratically on the wave function. So in the end, the Schrödinger equation contains linear but also cubic terms in the wave function. And with that, all hell breaks loose and the quantum mechanical toolbox no longer works.

Basically, all the ways to construct a gravitational field from the wave function directly will add a deterministic non-linearity in the Schrödinger equation. So what classical object can one construct in quantum mechanics that does not create problems? Within the orthodox formalism, there is one clear candidate: measurement outcomes. An experimentalist can measure a quantum system and then apply some control on the system depending on this outcome. One can see the classical outcome as acting on the quantum system. This is an example, albeit quite trivial, of consistent quantum to classical to quantum influence. To source the gravitational field, one could just measure some operator corresponding to the mass density and use the outcome as the source of the gravitational field. By construction, this will yield dynamics consistent with the quantum mechanical toolbox because it is formally just measurement + feedback. Obviously, one should not imagine that this measurement is done by a real physical observer. The new unorthodox dynamics should be “as if” someone where doing that within orthodox quantum theory. Interestingly, this is just what collapse models do (without the feedback step).

For discrete collapse models like the Ghirardi-Rimini-Weber (GRW) model, the equivalent of the “measurement outcome” is just the space-time event corresponding to the center of the collapse or the “flash”. For continuous collapse models, an equivalent can also be constructed and corresponds to what people call the “signal” in continuous measurement theory. However, for continuous collapse models this quantity was not historically introduced so it is a bit harder to explain how one should source gravity in one sentence. This brings us to a pedagogical difficulty that ultimately motivated the writing of the preprint. With Lajos Diosi, we have discussed the continuous models only because the resulting theory of gravity looks more appealing in this form. But again, in this context, the good object (this “signal”) to source gravity had not been previously introduced in the context of collapse models. As a result, in all my presentations, lacking time, I had to say that the idea was basically to source gravity from “the continuous equivalent of the discrete GRW flashes”. This is arguably unclear.

In July, I was attending a very nice school on philosophy and physics in Saig, Germany. I presented the work I did together with Lajos on semi-classical gravity. As usual I said that the main idea is to source gravity from the “continuous equivalent of the flashes of discrete models”. In the discussion, the philosophers (mostly David Albert if I remember correctly) told me it would be much easier to just do everything with the discrete model that people know. So this is what I did. I took the GRW model instead of the continuous ones and used the flashes as the sources of the gravitational field. I thought I would run into divergence problems but I did not. The resulting model is quite simple and the main equations are straightforward to obtain (although the final master equation is perhaps less transparent than the one obtained for continuous models). I do not think it provides a better theory of semi-classical gravity than the earlier ones but it gives a working theory of semi-classical gravity that has the same basic features and that is easier to obtain.

From right to left: Barry Lowers, David Albert, Nick Hugget and myself

At the conference, after the talk, Shelly Goldstein asked me if I really believed in these semi-classical gravity proposals (that is, either the continuous ones or the [yet to be written at the time] discrete one). To be honest, I would only put a very low probability on them. What I think they achieve is prove that it is not impossible to construct a theory in which gravity is fundamentally semi-classical (in the Newtonian limit) and in which there is no measurement problem. Probably nothing more.

update 21/09/2017: Anil Ananthaswamy has written a nice article on this preprint for Newscientist. I totally agree with Klaus Hornberger’s assessment reported in the article: the approach is interesting but has severe limitations so far.

This time, two very recent preprints about the black hole information paradox and a neat mathematical problem.

—(Information) Paradox Lost
by Tim Maudlin, arXiv:1705.03541

What if the reason the black hole (BH) information paradox has been discussed for so long is that there is actually no paradox to solve? What if people are just providing conjectural answers in “need for a question“? Tim makes a very convincing case that the paradox vanishes once things are properly defined and understood. This is an archetypal example of a situation where the clarity of mind of a serious philosopher of science should be stimulating for the physics community.

A lot has been written on the BH information paradox already. To be honest, I have never really understood the fascination of the community for this problem. I have tried to understand many times why the problem was so pressing, but the arguments I found were rarely if at all convincing. Trying to genuinely understand the paradox is annoyingly complicated by the fact that a large fraction of the folklore in the field is not supported by the literature: some options are dismissed as “provably” inadequate, but the proof cannot ever be found anywhere.

Tim’s preprint is welcome as it states the (alleged) problem in very clear terms and does so in a slightly provocative style that is very pleasant to read. The diffusing of the paradox is surprisingly simple: we see a spurious tension between (orthodox) quantum theory and relativity in the context of BHs because we are not applying the former theory properly. More precisely, the loss of unitarity in quantum mechanical dynamics in the presence of an evaporating BH can be traced back to the fact that we do not consider Cauchy surfaces as we should. The final hypersurface considered “after” the evaporation is typically not a Cauchy surface. Had we considered Cauchy-to-Cauchy maps, there would be no reason to expect any kind of problem.

Penrose diagram of an evaporating black hole. is a Cauchy surface, but is not –from Tim’s preprint

Tim provides successive refinements of his point and relates it with two theorems by Robert Geroch on the causal structure of Lorentzian manifolds. As Tim’s solution is quite simple, he needs to explain why the paradox has been so deeply misunderstood. He identifies, the problem, I think quite acutely, in a sloppy use of concepts that are intuitively clear but break down in the context of BHs. The section “But it no longer exists!” is excellent in this respect and refutes an objection based on a naive argument that I would have almost surely made (and that is, I believe, widely used in the literature). Along the way, Tim clarifies many important subtleties hidden in concepts such as information and observer (“from the point of view of observer A” may have many meanings).

Even if you doubt that a philosopher could bring something to a 40 year old physics problem, even if Tim’s point turns out to not hold for some subtle reason, his article is certainly a mandatory read for anyone interested in the BH information paradox.

— The grasshopper problem
by Olga Goulko and Adrian Kent, arXiv:1705.07621

Consider a given patch of grass of unit area but so far unspecified shape . A grasshopper lands at a random point uniformly distributed on this patch. Then the grasshopper makes a jumps of length in a random direction (with a uniformly distributed angle). Your objective is to maximize the probability that the grasshopper is still on the patch of grass after the jump. What is the optimal shape for the patch of grass that gives the highest probability?

The problem came to the authors because it is related in some subtle way to Bell inequalities but they realized the question was interesting in itself, because the optimal shapes are quite counter intuitive. Indeed, the naive disc shape can easily be shown to not be optimal, even for short jump distances (for , the disc is trivially suboptimal as ). The optimal shapes are weird, have interesting discrete rotational symmetry and there seems to be a phase transition at a well defined value of .

Phase diagram of the optimal grass patch as a function of the grasshopper jump size

The paper is a really nice as analytical estimations are mixed with thorough numerical explorations. I would not be surprised if it becomes a classic a bit like the sofa problem.

Ruwen Ogien, French philosopher, restless advocate of minimal ethics, died last week. Ogien was defending a conception of freedom, anchored in the harm principle of Mill, that seems today more needed than ever.

Ruwen Ogien © Kristiina Hauhtonen

Ogien has highlighted a minimalist definition of ethics which one can (grossly) summarize this way: just do not harm others, the rest is (morally) irrelevant. In this conception, there are no crime without victims and individuals have no moral duties towards themselves. To illustrate this principle in its most extreme and perhaps shocking consequences, it implies that drug abuse, suicide, incest (between consenting adults) and even necrophilia, although not advisable, should not be forbidden or at least not on moral grounds. Such an extreme minimalist understanding of ethics is clearly not without flaws and sometimes arguably naive, but Ogien has finely harnessed it to propose a remarkably seductive and emancipating libertarianism. In my opinion, it gives the strongest case for gay marriage, the legalization of drugs and of prostitution, or against the headscarf ban.

I have discovered the books of Ruwen Ogien too late, only roughly four years ago, with De l’influence des croissants chauds sur la bonté humaine (“Human Goodness and the Smell of Warm Croissants”), a profound yet entertaining book on experimental moral philosophy. Ogien made analytical philosophy cool. Philosophy is a game, you can ask questions, sometimes find answers, and even carry experiments. You need not let yourself smother by the bootstrapped bullshit of French theorists to attack hard questions: Ogien wrote in a sharp almost dry style, never hiding the weakness of an argument in convoluted prose. He popularized moral philosophy in the same way Dubner and Levitt popularized applied economics with Freakonomics. Extending the domain of ethics, he discussed pornography, love and ultimately illness. Ogien has greatly magnified my interest in moral philosophy and motivated my own vain musings on the value of life.

Just before dying, Ogien published Mes Mille et Une Nuits, an essay (that I have unfortunately not yet read) in which he discusses the cancer that ultimately killed him. According to the numerous reviews, this book is at the image of Ogien’s work: a quest to demystify and understand without compromise an issue usually deemed outside of philosophy. The conclusion: one does not reach any transcendence in illness, there is no beauty in suffering. This strikes me as similar to Houllebecq’s twist of Nietzsche’s quote “tout ce qui ne me tue pas me blesse et finalement m’affaiblit” (what does not kill me harms me and eventually weakens me). For individuals like me, intoxicated with the christian idea that you only ever strengthen yourself with pain, this is undoubtedly sobering.

There are very nice online resources to get a better idea of who Ruwen Ogien was. To mention only a few:

• A video interview about his latest book Mes Mille et Une Nuits
• A video interview about his book on love Philosopher ou faire l’amour
• An beautiful obituary by Sophie Dufau
• A short biography in Libération by Robert Maggiori

I would like to start bringing to the attention of my (almost inexistant) readership some articles/preprints which I have particularly liked. The objective is to put forward works that may have been overlooked or that are original in some way. As I have never done such a thing in the past, I have a huge backlog of articles to consider and thus no lack of inspiration. To keep this post decently short, I chose to start with only 3 papers but in wildly different fields: stochastic thermodynamics, philosophy of physics and quantum optics.

1 — Hidden Markov models for stochastic thermodynamics
by John Bechhoefer (2015) New J. Phys. 17 075003 arXiv:1504.00293

This articles introduces Hidden Markov Models (HMM), a framework that is well known to probabilists but usually ignored by physicists and that, to my mind, is extremely useful to understand stochastic thermodynamics and especially information powered engines (Maxwell demons). A HMM is simply a model in which there is a fundamental yet unknown Markov process randomly jumping from one site to another of a discrete finite graph. It is “hidden” in the sense that we only have a partial information on the process. One is typically given a series of imperfect observations and the whole game is to reconstruct the “best” estimate of the process position at some time (a priori or a posteriori) given these partial bits of information. The important thing in this framework is that there can be two sources of randomness: the fact that the fundamental process is intrinsically random and the fact that its state is not even perfectly well known (some heat related randomness and some “informational randomness). John Bechhoefer explains very clearly why this is the correct framework for stochastic thermodynamics and how to compute the basic quantities one is naturally interested in in this context. It is a good pedagogical article (requiring basically only undergraduate notions) that gives a clear conceptual underpinning to methods that are routinely used in stochastic thermodynamics. In my opinion, extending this formalism is the key to construct a meaningful theory of quantum stochastic thermodynamics.

2 — Against fields
by Dustin Lazarovici (2016) PhilSci-12862

Are fields really necessary as fundamental objects in physics or are they just useful computational tools? In this very nicely written article, my friend Dustin explains in a crystal clear way why it is entirely possible (and in his mind preferable) to abandon fields and keep only particles. The core idea, if I may caricature it this way, is that fields appear when one tries to rewrite globally defined dynamics as Cauchy problems, i.e. as problems with a solution that can be propagated forward in time. What Dustin shows is that fields can be seen as no more than book-keeping tools. As a result, they are sometimes helpful but can also yield problems, such as divergences, the latter being pure artifacts of their introduction. To illustrate his point, he considers the (unfortunately) not so well known Wheeler-Feynman formulation of classical electrodynamics which provides a global formulation of electrodynamics without electromagnetic field (incidentally, the article gives an excellent ressource to learn the basics of the W-F approach).

interaction forward and backward in time along the light cone in Wheeler-Feynman theory, from Lazarovici

All in all, I think Dustin makes the best case there is for a minimalist ontology of particles (at least for classical physics). Of course, as I have recently been working on approaches based primarily on fields, either for QFT or semi-classical gravity, I think a case can be made for fields as well (especially when fields obey non-linear equations, as is the case for gravity, it is harder to remove them from the picture with Green functions). But in the end I think the strongest point to know is that in many cases one can in principle understand everything without fields. Whether one ought to do so is perhaps slightly more open and provisionally a matter of taste.

As an aside, I think Dustin could have submitted a shorter version of this article to the latest FQXi essay contest, which deals with the tension between dynamical laws and teleological pictures (that is, pictures of physics in terms of final purposes). Although it is a bit of a stretch, one could defend the case (if only for the thought experiment) that the laws of Nature are ultimately always teleological (in a weak sense, that is written as global optimization problems on all space-time, I am not being religious), and that it is only the practical need to propagate some past knowledge about the state of things forward that forces upon us the use of dynamical representations and fields (and this is where one could use Dustin’s point). This is of course the kind of speculation I would find annoying in a regular scientific article, but it would seem suited for an essay (too bad the deadline was a month ago).

3 — Quantum trajectories for propagating Fock states
by Ben Q. Baragiola and Joshua Combes (2017) arXiv:1704:00101

This preprint has been posted very recently and thus my understanding of it is only a bit superficial but I think it could have important practical applications in quantum optics. Instead of the usual Markovian bosonic bath almost always considered in open quantum system theory, the authors consider a setup in which a quantum system of interest interacts with a propagating Fock state.

setup considered in the preprint by Baragiola & Combes

The entangled Fock state is then measured (with photodetection or homo/hetero-dyne detection). This gives a quantum trajectory for the quantum system of interest that can be computed explicitly. Although the machinery used is essentially that of “standard” continuous measurement theory, the result is a genuinely non-Markovian (and physically relevant) evolution that was not known before. The article is also nice in that everything is done explicitly with a solid introduction of the required formalism.

A tiny warning perhaps, the examples shown are a bit too simple to understand what can happen in the most general setting with the full-fledged theory (or at least this is my understanding so far, I would gladly be corrected). The fact that the total number of clics of the detector is equal to the number of photons in the incident Fock state comes from the interaction considered in the example (which is admittedly physically relevant). In the general case, the system can typically release an arbitrarily high number of photons into the field and solving the stochastic master equation requires, in principle, some truncation of the total Hilbert space.

The following entry is the translation of the appendix A of my thesis, initially written in french (French readers are thus invited to read it directly there). Surprisingly, one year after writing it, I still more or less agree with its content and thought it might be of interest to a broader audience, especially students and young physicists. I do not claim that it contains anything particularly new on foundations and is just aimed at taming the confusion that dominates the field, especially for beginners.

“Bohr brainwashed a whole generation of physicists
into thinking that the job was done 50 years ago. ”
Murray Gell-Mann

The existence of the problem

The foundations of quantum theory have an interest only if there is a problem to solve, something not every physicist is ready to concede (see e.g. Fuchs & Peres). Hence before doing the apology of a rigorous exploration of foundations, we should first convince ourselves of the seriousness of the preexisting problem.

The fundamental problem of the standard formalism of quantum theory is that is does not allow to derive the existence of a tangible and objective macroscopic world. A corollary, which is often the focal point of the debates, is the measurement problem, that is the impossibility to reduce the measurement postulate to unambiguous physical phenomena.

To my knowledge, there are two broad possible negations of the very existence of this problem:

1. the problem has already been solved by the “modern” theory of decoherence which explains in a satisfactory way the emergence of facts,

2. the problem comes from an outdated philosophical prejudice. There is no reality or, rather, talking about it amounts to leave the realm of science to compromise oneself with metaphysics.

In the first case, one admits the problem is real or at least has been, but one claims that it is solved by the theory of decoherence, which, because it can reasonably be considered to be part of the orthodox formalism, does not belittle its supremacy. In the second case, one criticizes the very legitimacy of the question using a lazy positivistic argument. It seems to me that those who remain unmoved by foundations are separated roughly evenly between these two categories or oscillate between the two lines of defense depending on the situation. It is useful to explain why those two arguments are inadequate; more precisely demonstrably false for the first and philosophically dubious for the second.

Decoherence

The objective of the theory of decoherence is to explain how the coupling of a system of density matrix 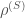with an external environment with a few reasonable properties yields the quick decrease of the non-diagonal coefficients of 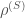in a certain basis. The theory of decoherence allows to understand both the speed at which coherences vanish and the choice of the basis in which 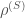is diagonalized. We should immediately note that this program has been a success (see e.g. [Zurek1981]). Zurek and his collaborators have shown, through difficult and undoubtedly elegant derivations, that the phenomenon is robust and universal.

Nonetheless, — and the profusion of new concepts such as einselection (for environment induced superselection, see [Zurek2000] or [Zurek2003] ) or the slightly pedantic Quantum Darwinism  [Zurek2009] changes nothing — decoherence only explains the diagonalization of 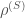in a certain basis and says nothing about collapse. Even if the main contributors to the theory rarely explicitly claim to solve the measurement problem, they unfortunately maintain the ambiguity, especially in articles aimed at non specialists [Zurek2014] .

Let us recall briefly why diagonalizing the density matrix is not enough. The mathematical part of most articles on decoherence consists in showing that in some more or less general situation one has:

It is known how to determine the basis of diagonalization and the latter agrees with what one would expect the pointer basis of the corresponding realized measurement to be. It is an undoubted success of the method: decoherence allows to explain what observable a given measurement apparatus actually measures, provided one admits that the latter collapses. At this stage, there is a philosophical leap that one should not do but that is often irresistible: identify the obtained diagonal density matrix, which corresponds to an improper mixture, with the density matrix coding for a true statistical (or proper) mixture. This confusion is what is sometimes called a category mistake in philosophy: two fundamentally different objects are abusively identified because their representation is identical. It is an error one would never do in any other situation. Consider for example an EPR state shared between Alice  (A) on the left and Bob (B) on the right:

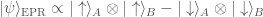
The reduced density matrix, from the point of view of Alice, can be written in a very simple way in the basis:

.

Does one conclude, in this situation, that the very existence of a part of the quantum state on Bob’s side makes classical properties “emerge” on Alice’s? Even assuming Bob’s state is forever inaccessible, the answer is clearly no. The object 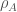cannot be assumed to be a statistical mixture without violating Bell’s inequality. In that case, identifying two physical situations because their mathematical representation is the same yields an obvious error. It is however the exact same substitution one does when trying to deduce macro-objectification from decoherence. The magical trick is usually done at the very end of the article, in a few sibylline sentences after long yet reasonable computations and thus often remains hard to spot.

We should note that this confusion around the claimed “foundational” implications of decoherence does not only have philosophical or metaphysical consequences and has given a fair amount of problematic extrapolations in cosmology and quantum gravity (see the references in [Okon&Sudardky] for a discussion). The situation nonetheless seems to slowly improve as the recent change of mind of Steven Weinberg on this matter shows; proving as an aside that even in this sensitive topic, smart people do change their mind.

Observables and perceptions as the only reality

Another option to refuse to seriously consider the measurement problem is to abide by an extreme form of positivism that can be caricatured in the following way. The objective of science being in fine to produce a set of falsifiable predictions, physical theories should only be formulated in terms of what is observable, talk only about results. Digging below the result, “microfounding” it, reducing it to a phenomenon would have no meaning because the result itself is the only thing that is objective. There is thus no difficulty with the axiomatisation of quantum theory that provides an algorithm that one knows how to implement in a non ambiguous way, at least for all practical purposes.

However, it is important to understand that such a vision of science is extremely restrictive and in no way implied, e.g. by Popperian epistemology. The fact that predictions are the ultimate product allowing to test or falsify a theory does not mean the latter cannot use a certain picture of reality as an intermediary, letting results emerge. Results and observables need not be primitive notions to be taken seriously. If this change of perspective were necessary, made totally unavoidable by experimental results, then one might understand or even justify such an instrumentalist attitude. However, as we will see, this is not the case. A point of view often belittled as classical is totally acceptable. Assuming that there is a world out there that exists in an objective way, measurements being only specific configurations of this world, is indeed in no way incompatible with the predictions of quantum theory.

A modern and trendy variant of the previous argument is to say that the only real thing is information (or, sometimes, quantum information, whatever that is supposed to mean), that the quantum algorithm is simply an extended probability theory that rules its exchange, reality being again in information itself. One may perfectly find that this point of view has merits as a heuristic guide, especially in the context of repeated measurements (and perhaps quantum thermodynamics). Yet, it seems impossible to take it seriously as information cannot be a primitive notion. Indeed, pure information does not exist and is a meaningless concept: one always has information about something. It is this “something” that one should define to make the approach rigorous; why not just do it?

A spectrum of solutions

Theories with a primitive ontology

Let us start by warning the reader that this section does not aim for comprehensiveness (for which one should rather check [Laloë]) and many approaches are voluntarily ignored. The objective is simply to present one possible way to construct theories that reproduce the results of the orthodox formalism without being plagued by its ambiguities.

It is possible that one finds very subtle and counter intuitive ways to construct reasonable physical theories in the future. In the meantime, one possible way, almost naive, is that of theories with a primitive ontology (see Allori et al.). It is only the modernized vocabulary of Bell’s proposal of local beables. Behind this uselessly pretentious word, which makes physicists draw their anti-philosophy revolver, lies an extremely simple notion. The ontology is simply what there is, physicists would say “reality“, Bell beables. The word “primitive” means that this ontology is the basis giving its reality to the rest and that does not require to be further explained in terms of more “primitive” concepts (such as the atoms of Democritus). It obviously does not mean that what one considers to be primitive cannot change as time goes by and our understanding of the world improves. It only means that what a given physical theory considers to be primitive should be precisely stated. One usually adds the constraint that this primitive ontology should be local, that is a function of space time (and not e.g. of configuration or phase space). A priori, nothing makes this constraint absolutely necessary, it simply allows to understand easily how macroscopic objects, that naturally live in space-time, emerge from the configuration of the primitive ontology. If doing this simplification is possible, i.e. always allows to construct consistent theories, then it would be stupid to not use it. We should note that there exists a wide variety of primitive ontologies that are a priori acceptable, that is, that allow to model the world: particles obviously, but also fields, why not strings, and more recently flashes.

Once the primitive ontology defined, the postulates of a physical theory should only prescribe its dynamics. The rest, observations, measurement results, all macroscopic behaviors, should be logically derivable as theorems. This is not revolutionary: classical mechanics –in which the ontology is simply the particles– fits perfectly well in this definition and no one would dare contest its scientific character. This approach, erstwhile awkwardly heterodox, seems to now be used by a larger and larger fractions of the physicists and philosophers interested in foundations because it makes discussions precise, essentially mathematical, and takes the debate away from philosophy. A theory based upon a primitive ontology is non-ambiguous and thus easy to discuss. No question is in principle forbidden as in the standard formalism; the theory somehow takes more risks than a pure “prediction” algorithm but is in return immediately intelligible.

We can now present very briefly (that is without proving that they work) 3 examples of theories with a primitive ontology that are compatible (up to ) with the predictions of the standard formalism of non-relativistic quantum mechanics.

The example of a particle ontology

The de Broglie-Bohm (dBB) theory, or pilot wave theory, has a very simple ontology: a given number of particules without properties or qualities move in space. Writing 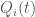the trajectory of the particle on has the following purely deterministic equation:

.

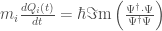The wave function 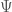(which can be scalar, spinor or vector valued) evolves according to the “standard” unitary evolution (e.g. Schrödinger, Pauli-Dirac,…) and can be considered to have a nomological (law-like) rather than ontological (real) status. That is, 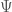guides particles as a law and possesses a status similar to that of the Hamiltonian in classical mechanics (which prescribes the trajectories without being determined by them). It has been shown, and it is the product of a long work of physicists and philosopher because the result is not trivial, that this theory is empirically equivalent to the quantum algorithm so long as the predictions of the latter are not ambiguous (see e.g. [Berndl1995], [Dürr2009] or [Bricmont2016]). Hence, there exists a precisely defined theory, in which position and velocity are always well defined, in which the observer is a physical system like any other, that is fully deterministic and in which all the quantum weirdness can be reduced to a purely mechanical and causal (thus non-romantic) explanation.

The dBB theory should not be seen as an ultimate approach to adopt or fight, but rather as a particularly clear and simple prototype of what a theory with a primitive ontology may look like. It is however not the only one and objective collapse theories can also be put in such a form. In that latter case one can have either a primitive ontology of fields or of flashes (one may also copy the dBB construction and put particles but we shall not discuss this option here).

Two ontologies for collapse models

Before discussing the ontology of collapse models, one should perhaps say briefly what they consist in (see e.g. the Stanford Encyclopedia of Philosophy). The idea of collapse models is to slightly modify the standard linear evolution for quantum states:

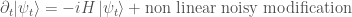
With this modification, the Schrödinger equation slightly violates the superposition principle. The modification can be chosen tiny enough that the standard quantum mechanical predictions hold for atoms and molecules but that macroscopic stuff is sharply collapsed in space. A typical example of such a modification is the GRW (from Ghirardi Rimini and Weber) model in which the wave function has a tiny objective probability to collapse into some sharper function:

The rate is small enough that atoms never encounter such collapses but that macroscopic bodies are constantly kicked towards well localized configurations in space. This, however, is not enough to solve all the problems with quantum theory. After all, the only object we still have is a wave function in configuration space, a very non-local object, hence definitely not a primitive ontology. A possibility to project down the wave function to a primitive ontology is simply to consider the mass density field:

,

where is the mass density operator. This gives a continuous matter field living in space that we one can consider to be what is real in the theory. One then realizes that it is possible to account for all experimental situations (i.e. even spin measurements) in terms of fluctuations of this field. The wave function is then only a convenient computational tool to write the dynamics of the primitive ontology in a compact way. Of course, there are clearly many other possibilities but taking the mass density allows to readily understand the localization of macroscopic objects.

Another option is to take the flashes, that is the centers of the collapsed wave functions after a collapse event, as the primitive ontology. One obtains a collection of space-time events, localized in space and in time, thus providing a very shallow reality. However, it is also possible to convince oneself that the world (with tangible tables and chairs) emerges at the macroscopic scale from this ontology in the same way as one sees the landscape only after zooming out from a pointillist painting.

The difference between these two collapse approaches and the dBB theory presented previously is the existence of some fundamental randomness in Nature: the two ontologies of collapse models contain a stochastic component, in the classic sense. On top of this, collapse models add some instrinsic decoherence which makes them slightly different from orthodox quantum mechanics (instantiated in the Standard Model) with respect to experimental predictions. These models can obviously be criticized for being ad-hoc and excessively fine tuned but one cannot deny that they are defined in a precise way without any reference to an observer.

One could worry, and actually one often worries, that there exists many possible primitive ontologies providing theories with the same empirical content. Does not it mean that ontologies are meaningless? Of course not, whatever the theory (not necessarily related to quantum mechanics) there will always exist infinitely many possible realities to explain a given set of results. The particle ontology of classical mechanics is empirically indistinguishable from an ontology of tiny angels, constantly breaking down and moving pieces cut from a continuous matter, miraculously reproducing the results of Newton’s laws. Does it imply that the ontology of material points needs to be abandoned in classical mechanics? That talking about atoms is bound to be meaningless? Of course not, choosing between different primitive ontologies can be made with the help of Occam’s razor that cuts through the invisible angels. One should not misinterpret Russell’s teapot argument: the existence of a teapot orbiting Saturne is not falsifiable but it does not mean that every ontology that does not directly manifest itself to our senses should be dismissed. We have no reason to believe in Russell’s teapot, we have some to believe in reality.

A few benefits of a demystified theory

Even if the reader is convinced that the previous program solves an actual physical problem, she may still question the practical use of the proposed solution. Has the orthodox approach not enabled tremendous technical progress? Why would the “shut up and calculate!” of Mermin be less legitimate today if one only care about what is true for all practical purposes? The objectif is now to show that from a purely opportunistic and pragmatic point of view, it is extremely profitable to have clear ideas about the foundations of quantum theory.

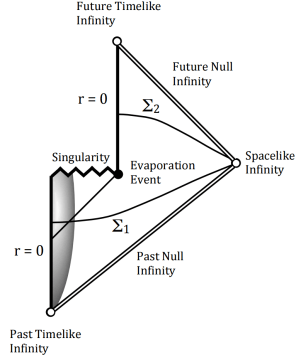
Having a class of precise theories reproducing the predictions of the orthodox quantum formalism provides a better basis (or at least a different basis) to generalize the theory, say to gravity. In this example, one can think of coupling the primitive ontology of a collapse model to space time to unify gravity and quantum mechanics with a peaceful coexistence of quantum and classical sectors, thus providing another indication that gravity need not necessarily be quantized. This idea has motivated a recent attempt by Lajos Diosi and I in the Newtonian regime. If one insists on quantizing gravity, then the dBB approach, explored notably by Ward Struyve (see previous post), shows on a few toy models than one can give a precise meaning to space-time and its singularities in a non perturbative way (where the orthodox approach requires many layers of interpretation to understand an “emergent” space-time). This constatation may be only anecdotal, but it seems that collapse models provide an extremely intuitive way to couple quantum particles with a classical space time without really simplifying the situation if gravity is to be quantized as well. On the contrary, Bohmian mechanics seems to be unable to do a consistent semi-classical coupling but allows to easily construct toy models in which gravity is quantized. Foundations thus offer a guiding perspective to construct the future unification of the two long separated sectors of modern physics.

In more precise examples putting together gravity and quantum theory, theories with a clear primitive ontology have already allowed significant advances. The problem of fluctuations in inflationary cosmology [Sudarsky2009] has been much clarified by toy models of collapse (see again [Okon&Sudardky] and references therein) and theories inspired by dBB [Goldstein2015].

The research in foundations has also produced useful byproducts such as powerful numerical methods inspired by dBB [Struyve2015], notably used in quantum chemistry [Ginsperger2000] [Ginsperger2004]. The most important result discovered fortuitously thanks to foundations is no doubt Bell’s theorem. Indeed, John Bell, having realized that the impossibility theorems of Von Neumann and Gleason on hidden variables proved essentially nothing –as the very existence of Bohm’s 1952 theory showed– wondered if the non locality of the latter was inevitable. As this fact is often not known and often deemed surprising, let us cite Bell in “On the Problem of Hidden Variables in Quantum Mechanics”, published in Rev. Mod. Phys. in 1966 and which was written before the discovery of his inequality:

“Bohm of course was very well aware of the [non locality problems] of his scheme, and has given them much attention. However, it must be stressed that, to the present writer’s knowledge, there is no proof that any hidden variable account of quantum mechanics must have this extraordinary character. It would therefore be interesting, perhaps, to pursue some further ‘impossibility proofs’, replacing the arbitrary axioms objected to above by some condition of locality, or of separability of distant systems.”

A last paragraph which can be read as a program…

Reasoning in terms of primitive ontology may also be a way to bypass the difficulties of the reasoning in term of state vectors or operator algebras. Having a clear primitive ontology (in this case, flashes) is what allowed Tumulka to construct in 2006 a fully Lorentz invariant collapse model (without interactions) where such a result would have been hopeless at the wave function level. The resulting theory has no simple expression in terms of operator algebras but reproduces the predictions of quantum theory (up to ). Bypassing the state vector may also give ideas to overcome the difficulties in defining rigorous quantum field theories with interactions [note: this is what later motivated this work]. Indeed, one may very well understand that a law (e.g. the value of a two point function) can be obtained through an iterative procedure, as a limit of something via the renormalization group. But it is the fact that the objects themselves can only be seen as limits that poses important mathematical problems. One may imagine that we some day have a well defined theory with a clear primitive ontology that only requires renormalization arguments to compute the dynamical law of the ontology, but not to define it. Instead of thinking the algebraic structure of quantum theory as primitive, as it is usually the case in axiomatic approaches to QFT, one may hope to obtain it as something emergent, from the dynamics of a primitive ontology (thus possibly bypassing some impossibility theorems). This is of course extremely speculative, but our purpose is just to argue that foundations may also have an interest in mathematical physics.

Finally, a major interest of the clarification of quantum foundations is to liquidate an important number of prejudices that encumber modern physics, philosophy, and sometimes even the public sphere. One may very well hate dBB theory and prefer the orthodox formalism (that may even be preferable if one wants to do computations). However, the very existence of dBB, a theory that is compatible with all the predictions of quantum mechanics, makes many commonly held view about the purported epistemic implications of the quantum paradoxes manifestly inaccurate. Quantum mechanics does not imply that Nature needs to be fundamentally random, it does not imply that the observer is necessarily inseparable from the observed system, it does not imply a role of consciousness in any physical process, it does not forbid in principle the use of trajectories nor does it makes the simultaneous definition of position and velocity impossible (it forbids to observe them); it does not finally imply the existence of multiple universes. In the end, quantum theory demands almost none of the epistemic revolutions it is assumed to require. The only provable implication of quantum mechanics (experimentally verified) is the need for some form of non locality, but it is rarely this feature (absolutely unsurprising for the public) that is put forward. Physicists, without bad intentions, usually like to emphasize the mystery. A positive effect is to cover the field with a glamorous glaze and, perhaps, to improve its funding and attractivity. However, this does not go without risk and such a behavior blurs the line between science and pseudo science. The proliferation of New Age literature lending absurd virtues to quantum mechanics would seem like a laughing matter. The disturbing fact is that what one can read in those books is not so different, at least from the point of view of the public, from the things serious physicists may say during popular conferences.

Quantum mechanics is too important to neglect its foundations. A few simple results strongly clarify the status and implications of the standard formalism. Knowing them can help one feel better with the theory (which is not negligible for students) and also help get new ideas to extend it or prove new mathematical results. Having many viewpoints on the formalism also helps liquidate the misconceptions that physicists have unfortunately exported to philosophy and sometimes carelessly communicated to the public. Finally, there is no good reason to leave foundations to the exclusive attention of retired theorists…

My preprint “Interacting quantum field theories as relativistic statistical field theories of local beables” has just appeared on arxiv. Fortunately, even with the few bold claims that I made, I have not been flagged so far by the algorithmic crackpot detector and my paper went through without difficulty. As I had emphasized in the previous post, for once it is a work I am very proud of. I do not know if every single detail will hold closer scrutiny, but at least I am confident that the main message is correct and should be of interest to people working in quantum foundations (on the pure theory and phenomenology sides).

Last week, I had the pleasure to be visiting Lajos Diosi in Budapest. We made some progress on the semi-classical gravity front and on the quantum feedback front which will probably materialize in the form of preprints in the not so distant future. It was a great but tiring trip: discussing physics non-stop, from dawn to dusk, is really mind wrecking.

Budapest

As an aside, I went from Munich to Budapest and back in bus (Flixbus) and it is a quite smart way to travel. Sure, it’s long, 8h30. But most of the time is productive. The bus had power outlets and excellent wifi and I thus managed to work, answer emails, watch movies. On my way to Budapest, I took the night option and slept almost all the way through, effectively teleporting myself instantly. It is also cheap and does not pollute much, so I would definitely recommend. In France, long distance bus lines have been authorized for only a few years which is why I have only realized this option existed recently. They were previously forbidden to provide SNCF with a monopoly. I think the argument was that a railway is essentially operated at fixed cost and, as a result, it may be optimal to nudge or even force people to use train to reach the point where the cost per passenger drops bellow that of all other means of transportation. This global optimum can be reached for fast lines (TGV) between Paris and big cities (France railway network is a star graph) but it is clearly impossible for two medium sized cities that are far from each other (say, Rennes and Toulouse). In that case, the railway monopoly was arguably harming the mobility of people. I think the situation is now closer to an optimum with two networks: a (mostly) star graph of fast TGV connections with Paris in its center, and a slower but fully connected graph of bus lines between medium sized cities.

French train network and its trafic in 2007

Before going to Budapest, I spent two days in Paderborn, invited by Martin Kolb, a probabilist. He has been recently specializing in the study of one of the concepts of stochastic calculus I find the most subtle: the local time . It is the time the Brownian motion spends at a given point (typically 0). Of course, it is defined appropriately, as a rescaled limit of the time spent from 0 so that the result is not trivial. This is a concept I had been introduced to during my thesis when I was studying quantum spikes with Michel Bauer and Denis Bernard and I still find its properties quite counter-intuitive and sometimes mysterious ( is a Levy process, so weird stuff happens when switching from real time to local time). Martin showed me interesting results on Brownian motions conditioned through constraints on its local time. The corresponding paper is published in Annals of Probability (also on arxiv), and the reader interested in probability theory should have a look.

Paderborn

Now back in Munich and with my long-term work on foundations now packaged in a preprint and online, I hope to work a bit on subjects closer to the main interests of the group. My objective is to understand better tensor network methods in the continuum. The dimension 1 is very simple but has been widely studied already so I would like to attack the 2 dimension case. Brute force generalization of the discrete case is possible but super formal and does not seem to allow to compute anything, but maybe one can be smarter and construct continuous ansatz that have no discrete counterparts. In an unrelated subject and back in foundations, I am also thinking about writing a note on Lorentz invariant noise. It seems to me that there exists no article on what are the properties of Gaussian processes and point processes that have a Lorentz invariant probability distribution. I think I now have a crude classification of what one can get and so it might be helpful to write a short note about it. If anyone can provide existing references about this kind of stuff, a comment would be most helpful.

I have been working on an ambitious project for quite some time and, although there are still questions to be settled, I think the main lessons are now robust enough that they can be profitably discussed. I have a draft (modified 09/02/2017) which I will put on the arxiv (update: it’s now on the arxiv) once I get some feedback (and likely tame some bold claims that may not be as firmly grounded as I first thought). Comments are of course very welcome. As I have also made a first presentation of the results at the seminar of the group of mathematical foundations of physics at LMU, I have some slides that give a short (and thus inevitably provocative) overview of my claims.

So what is this all about? I think I have (at least partially) succeeded at constructing simple collapse models in a quantum field theory context. This would already be enough to make me happy, but what gets me really excited is the fact that this construction yields what I think are quite important lessons about both QFT and collapse models.

As everyone knows, quantum field theories are not about fields, at least not in the usual sense. There are no “tangible” fluctuating fields in QFT. One can perhaps write QFT as a dynamical theory of wave functionals on field configurations, but one certainly cannot see QFT as a statistical field theory on . In its very formulation, QFT is an operational theory, that is, not a theory about microscopic “stuff”, but ultimately a theory that says things about the statistics of measurement results, ie of very macroscopic stuff. QFT, as well as other quantum theories, is agnostic about what the microscopic stuff could be (which sometimes leads people to think that there is no microscopic reality, whatever that’s supposed to mean, but this is obviously not a logical implication).

Unfortunately not a quantum field

In non-relativistic quantum mechanics, there is a way (among other reasonable options) to make the theory about microscopic stuff: collapse models. The idea is to modify the Schrödinger equation a bit to collapse macroscopic superpositions without changing the predictions of the theory too much (but there is of course a modification involved). Collapse models give a stochastic evolution for the wave function that, although admittedly ad hoc, gives a behavior that looks more reasonable. Small things can be delocalized, big things, such as a measurement apparatus, are always well localized. The theory is still not about stuff in physical space but one can define “local beables” (that is some field/particle in physical space one takes to be real) and see collapse models as dynamical theories of this stuff. So, in a nutshell, collapse models allow to rewrite non-relativistic quantum mechanics as a theory that is specific about what the microscopic world is made of. The price to pay is that the empirical content of quantum mechanics (what it says about the statistics of measurements) is modified. For that latter reason, collapse models are currently under intense experimental scrutiny.

Now, what I have constructed changes the two previous stories in a substantial way. I propose a relativistic collapse model that has two important features:

• It is naturally written as Lorentz invariant statistical field theory (i.e. a theory of random fields on ).
• It is empirically equivalent to QFT.

That is, QFT can be written as a theory of fields in the usual sense after all, and collapse models can be completely “hidden” or embedded within an existing quantum theory. Better, it is the same model that does those two things.

To my mind, this has important implications for QFT and collapse models. First, for collapse models, one might want to slightly reconsider the efforts that have been invested in phenomenology (and thus I must respectfully disagree with the latest blog post of Sabine Hossenfelder, where she advocates for more phenomenology in this context: I think this time we need a bit more “talk” before.). Indeed, if collapse can reasonably be hidden in existing sectors of the Standard Model, it means that the effects we currently consider to be typical signatures of collapse just come from peculiar choices of non-relativistic models. Collapse models really can be seen as an interpretation of quantum theory (where interpretation is taken in the slightly improper sense it has nowadays, that is as a complete theory underlying the operational formalism of quantum theory without modifying its predictions, insofar as the latter are well defined).

One the QFT front this may also give interesting things. The reformulation of QFT I obtain takes the form of a statistical field theory on , that is I have a probability measure (or an object that is formally a probability measure) and the field that one draws from this distribution can be considered to be all there is: it is the final output of the theory (and then, further analysis yields the operational prediction rules, but the latter are not primitive). The nice thing with a probability measure, and more generally about a theory that gives dynamics for “stuff”, is that it can be modified at will without becoming logically inconsistent. This is to be contrasted with an operational framework that may become self contradictory after the slightest modification. Why is this helpful for QFT? Because of the need for regularization. QFT nastily diverges. This is why one usually does computations with a regularization framework before sending the cut-off to infinity (which then requires to redefine the parameters and renormalize the theory, but renormalization is something in spirit that is very different from regularization). But why can’t we just consider regularized theories right from the start, say that they are the real thing, and then just say the cut-off is far so we devise approximation schemes to compute predictions? In this picture, renormalization would then simply be a method to relate the bare parameters of the model to what one measures, without any “fundamental” character. The issue is that, to my knowledge, regularized QFTs are never QFTs. To regularize a QFT one needs to cut the higher momenta. This can be done by putting a lattice (as in Lattice Gauge Theory), but then it’s neither a field theory nor a Lorentz invariant theory. To cut higher momenta in a covariant way, one would typically need higher derivatives in the Lagrangian. But because of Ostrogradsky’s instability, one cannot canonically quantize the corresponding theory. It is nowadays popular to say that QFTs are effective theories as a way to explain out the issues one usually encounters in the UV (such as the Landau pole of QED). However a QFT cannot be the effective theory of its regularized version as the latter cannot be fundamental. This explains (a small part) of the appeal of String theory that does have a UV cut-off without the need to break invariances.

Once QFT is defined as a classic probabilistic theory of fields, regularization is a perfectly legal thing to do. Cutting-off covariantly the highest momenta in the propagators, say by Pauli-Villars regularization, can be done at the fundamental level. In this new formulation, a regularized QFT is a QFT, and a thus a possible well defined foundation of physics.

Of course the draft is just of first exploration of this idea and I don’t want to hide the technical difficulties that are still in the way. There is certainly still a lot of stuff to be done, especially at the quantitative level, to know how fast exactly the reduction of superpositions through the collapse mechanism occurs. The level of mathematical well definiteness of the objects used in the theory, even after regularization, certainly needs to be discussed thoroughly as well. Nevertheless, I remain very happy about this result as it seems to me that it opens a whole range of new possibilities.

update 9/02/2017: I have put a newer version of the draft. I had made a mess in the functional integral representation trying to be clever with sources so I have now rewritten everything in terms of asymptotic fermionic states. Hopefully, it now makes more sense.

update 22/02/2017: The preprint is now on arxiv. I am glad I was not flagged by the algorithmic crackpot detector. Hopefully, this will provide me with feedback from a wider community

I have just posted on the arXiv a new preprint (a short letter) about a recent work of mine on non-Markovian stochastic Schrödinger equations. It is an unexpected technical byproduct of a more fundamental and long term research effort to construct tractable relativistic collapse models (but it will likely not seem related at all). Before explaining what I did in this preprint, it is probably worthwhile to recall a few things about stochastic Schrödinger equations and their history. This will be a rather technical entry but as the preprint itself is about something technical, there is no point in making a summary for a broad audience.

The most well known objective of stochastic Schrödinger equation is to unravel an open-system evolution. One typically considers an open quantum system of density matrix with a Markovian evolution generated by a Linbladian :

An unraveling of this open evolution is a random evolution for pure states such that the open evolution is obtained as the probabilistic average of the pure state trajectories:

.

The interest of this rewriting becomes obvious for large systems. Indeed, one needs quadratically more memory to parametrize a density matrix than to parametrize a pure state and it is thus preferable to work with the latter in numerics. The price to pay is of course that an averaging is needed in the end and the stochastic pure states are thus often called “Monte Carlo wave functions” in this context.

Now, given a specific Lindbladian, I did not say what the evolution equation for the pure state was. Actually, there are infinitely many possible stochastic pure state trajectories, jumpy or diffusive, unraveling the same Lindblad equation. I can still show an example. For a simple Lindbladian a possible diffusive (linear) unraveling of the open evolution is given by:

,

where is a Wiener process, i.e. a normalized 1d Brownian motion. It is easy to check that with this evolution verifies the unraveling condition (if it does not seem to work, remember the “physicist” Itô rule ) . The pure state evolution at this stage is still linear but the downside is that it is not norm-preserving (the generator is clearly not Hermitian). This is an issue for numerical simulations because the norm of almost surely converges to zero. The statistical average is then dominated by rare events that have a with a huge norm; we hit the so called “importance sampling” problem: most of the states that are sampled are useless. One can be more clever and find, with a bit more work, a non-linear diffusive unraveling that is norm preserving:

where and I have chosen  to simplify. Knowing only the previous linear unraveling, it is not so trivial to find this non-linear version (the standard technique is to normalize the linear state and then transform the probability measure to preserve the unraveling condition). Nonetheless, all these (Markovian) unravelings, linear or non-linear, once they are known, share a nice feature: they are explicit and trivial to solve numerically (typically by discretization, naive or more elaborate). All is great in the Markovian realm.

Before I jump to the non-Markovian regime, it is important that I mention the other applications of stochastic Schrödinger equations, especially as my own result does not have much interest without this context. Although it is their use in numerics that made stochastic Schrödinger equations famous (especially the 1992 article by Dalibard, Castin and Molmer in the jump case), the equations were actually discovered earlier (in the mid eighties) by people trying to understand the foundations of quantum mechanics. The objective was to find modifications of the Schrödinger equations that would spontaneously project the quantum state in measurement situations without having to use the collapse postulate (this gave rise to the so called collapse models which I may discuss in more detail in the future). The Markovian equations that were found to be consistent are stochastic Schrödinger equations of the same form as those used for unravelings. Roughly at the same time, physicists and mathematicians studying continuous measurements also discovered the same equations. In that case, the unraveled process is “real” in the sense that it describes a quantum trajectory associated to an actual measurement readout. In that latter case, a nice thing is that one gets the non-linear equation immediately without having to guess or use subtle changes of probability measures. Hence finally, stochastic Schrödinger equations can be used as a numerical method for open quantum systems, as a hypothetical solution to the measurement problem, or as a way to understand actual continuous measurement situations in the lab.

This rather “multifaceted” success in the Markovian case immediately suggested to look for a generalization to the non-Markovian regime (i.e., with the unraveling picture in mind, for a bath with memory). This was done in the late nineties with only a small subtlety for the continuous measurement application. Non-Markovian stochastic Schrödinger equations were indeed found to not yield true observable real-time trajectories but only trajectories obtainable point by point a posteriori. This difficulty of interpretation (which gave rise to quite a few papers) is unfortunately not the biggest issue in the non Markovian realm. The biggest problem is that, except in some very specific cases, it is impossible to compute the solution of a non-Markovian stochastic Schrödinger equation, even numerically. This is because the equation possesses a memory term involving a functional derivative which is essentially impossible to evaluate. People have developed perturbation techniques to approximate the solutions in some limit but no general purpose method existed (as far as I am aware). This is were my preprint may come useful: I propose a non perturbative numerical method to compute the solutions of non-Markovian stochastic Schrödinger equations.

I find the method quite cute because it uses a sort of unraveling again. In a nutshell, the trick is to write the solution of the non-Markovian stochastic Schrödinger equation as the statistical average of another state that obeys a simpler stochastic equation:

,

where is the simple auxiliary state. At that point, to give the details I would need to explain how one constructs general non-Markovian stochastic Schrödinger equations in the first place. Luckily I do this in the aforementioned preprint so at that point it is probably easier to simply just read it, especially as it is pretty short and self-contained.

Now I should be transparent about the limitations of my proposal. The method works well for linear stochastic Schrödinger equations but the extension to the non-linear ones is admittedly ugly and not of much help, as it relies on Metropolis sampling. Consequently, it suffers quite heavily from the importance sampling problem and becomes dramatically inefficient for large times (compared to the effective system-bath coupling timescale). It should also be added that if the method is used to solve an open-system evolution (by two successive unravelings) then it is not new and it coincides with the technique developed in 2002 by Stockburger and Grabert. Hence the real novelty comes only if one is interested, not in open-system evolutions, but in the two other applications of stochastic Schrödinger equations: foundations and measurement theory. That said, it does clearly solve a problem that was particularly annoying: the seeming impossibility to even plot a mathematical object central to three subfields of quantum theory. Short term, this is enough to make me happy.

This entry is written in french as it deals principally with French idiosyncrasies.

Il y a quelques jours, l’Express a relevé un nombre assez alarmant de plagiats dans plusieurs ouvrages, chroniques et articles d’Étienne Klein, un vulgarisateur-philosophe populaire. Je tiens à préciser d’emblée que je n’ai pas d’antipathie particulière pour Klein. Même si sa tendance à se faire mousser, à se présenter comme un physicien professionnel qu’il n’est plus depuis longtemps, et à couvrir certains sujets simples de pédanterie verbeuse m’a toujours fortement agacé, il faut reconnaître que Klein est, ou était, un des meilleurs vulgarisateurs nationaux télégéniques (la concurrence étant, il est vrai, loin d’être rude). Mon objectif n’est donc pas de traîner Klein dans la boue : les faits sont suffisamment graves pour que d’autres s’en occupent et il tombera peut-être en disgrace médiatique pour un court instant. Je pense qu’il n’est pas utile d’ajouter à la charge. J’aimerais plutôt profiter de ce prétexte d’une possible recomposition du paysage de la “vulgarisation en physique française” pour tenter une réflexion personnelle sur le fond : qu’est ce que la bonne vulgarisation et comment faire pour en améliorer la diffusion en France ? 

Il n’est pas facile de définir de manière directe une vulgarisation (ou une popularisation) optimale de la physique mais on peut au moins en faire la théologie négative et éliminer ce qui n’en est pas. Les risques et travers principaux viennent de l’asymétrie de la situation : un physicien, en général le seul à savoir à peu près de quoi il parle, est mis face à un public contraint à la crédulité faute de connaissance sur le sujet. La physique regorgeant de résultats contre intuitifs et ces derniers étant en général ceux que l’on aime raconter, il est fondamental que le vulgarisateur ait la confiance totale de son public. Il est malheureusement trop facile de gagner cette confiance de mauvaises manières.

Le problème de la légitimité

La première manière contestable d’obtenir la confiance de l’auditoire est l’argument d’autorité : “je vous apprends des choses surprenantes sur le fonctionnement de la Nature, mais croyez moi sur parole : je suis un gros poisson dans le milieu, le Einstein du XXIe siècle.”. C’est un des péchés les plus courants et il n’est pas toujours évitable. C’est parce qu’ils y ont succombé que les frères Bogdanov se sont inventé des doctorats ou, dans une moindre mesure, qu’Étienne Klein se présente généralement comme un physicien théoricien actif alors qu’il ne l’est plus depuis presque 20 ans. Dans un autre domaine, le CV honteusement bidonné d’Idriss Aberkane est une illustration de cette tentation d’exagérer son influence pour acquérir la confiance du public à bas prix. On ne peut évidemment pas s’affranchir totalement de l’argument d’autorité et il est naturel d’accorder plus de crédit à un physicien influent et respecté dans sa communauté qu’à un parfait inconnu. Le problème est que s’il est assez évident pour un chercheur d’évaluer la crédibilité et l’influence d’un de ses pairs, la chose est presque impossible de l’extérieur. Aux États-Unis par exemple, Neil deGrasse Tyson est un vulgarisateur de premier plan en astrophysique mais on en déduirait trop vite qu’il est un physicien important. En réalité, pour les chercheurs en astrophysique, deGrasse Tyson est un parfait nobody : il n’a eu quasi aucune influence intellectuelle dans le domaine et n’a presque jamais été réellement actif en tant que chercheur. Et ça n’est pas, a priori, un problème ! Le tout est que la présentation des concepts et des théories qu’il fait au public soit honnête (et dans ce cas précis, j’avoue ignorer si c’est le cas).

Comment la confiance se gagne-t-elle donc légitimement ? C’est une réponse peut-être un peu décevante mais il me semble que la seule bonne manière d’inspirer la confiance est de présenter les concepts avec rigueur et honnêteté. Le vulgarisateur ne devrait idéalement pas chercher à étaler ses faits d’armes.

Du point de vue du public et des médias, si le vulgarisateur a l’air de savoir de quoi il parle, il faut bien un critère pour filtrer les beaux-parleurs. On peut alors utiliser les quelques métriques imparfaites d’influence (h-index, publications récentes dans des revues à comité de lecture, avis d’autres chercheurs du domaine). Rien de tout cela n’est infaillible mais fournit au moins un moyen d’éliminer les crackpots (on peut aussi passer l’apprenti vulgarisateur au détecteur de quacks ou au crackpot index)

Le problème de l’hubris

Un deuxième travers est d’essayer d’en mettre plein la vue à son auditoire pour gagner son admiration. Un grand nombre de phénomènes en physique, en particulier en relativité et en mécanique quantique, ressemblent à des tours de magie. Il se passe quelque chose de contre intuitif, presque choquant et qui attire immédiatement l’attention. C’est positif et c’est en partie ce qui fait que la physique est intéressante. Mais il ne faut pas perdre de vue que l’objectif est in fine de comprendre l’astuce; le magicien doit ici expliquer le tour sans quoi il ne fait que mystifier l’auditoire (ou le lecteur) sans rien lui apprendre. Il doit rendre des résultats complexes intelligibles et dissiper le mystère initial, pas le renforcer en tombant dans le sensationnalisme. Le risque est de sauter de surprise en surprise, de résultat “qui claque” en mindblowing fact par facilité, sans jamais présenter ce qui fait le cœur du travail du physicien : l’entreprise inlassable de réduction du domaine de l’incompréhensible. Pour forcer le trait, le rôle du physicien, et je le pense aussi du vulgarisateur, est de lever si bien le voile que la surprise initiale devienne après analyse presque décevante, comme lorsque l’on comprend que le prestidigitateur avait notre carte dans la main depuis le début du tour. Le phénomène n’en reste pas moins saisissant, mais ce qu’il y avait d’irrationnel ou incompréhensible a été purgé. Le problème est évidemment qu’il est infiniment plus valorisant pour le vulgarisateur de se dispenser de la seconde phase de démystification. En effet, en entretenant l’obscurité, il s’accorde un rôle privilégié d’oracle : “vous voyez, le monde n’a aucun sens, sauf pour les rares élus qui comme moi ont vu à travers le voile : écoutez/lisez moi religieusement”. C’est une position très agréable pour l’ego et qui est par conséquent souvent irrésistiblement attractive. De manière perverse, le bon vulgarisateur se rend de moins en moins nécessaire alors que le mauvais se crée une communauté de disciples.

Face à cet état de faits, le public a un rôle important à jouer. Il doit oser se poser la question : ai-je appris quelque chose, ou m’a-t-on fait rêver un moment sans me donner aucun moyen de comprendre ? Le mystère s’est-il épaissi ou ai-je acquis une meilleure compréhension de ce qui se passe ? Si le mystère n’a pas diminué, est-ce au moins parce-que j’ai mieux saisi la complexité des phénomènes en jeu ? Répondre par la négative n’est pas forcément facile : on a toujours l’air idiot lorsque l’on concède ne pas avoir saisi la profondeur supposée d’une oeuvre absconse. C’est néanmoins nécessaire pour dissuader les charlatans de servir toujours la même hype creuse. Il faut aussi se méfier des physiciens respectables qui sont souvent paradoxalement friands de mystère. Le “publish or perish”, s’il n’a pas toujours que des effets négatifs et dynamise certainement la recherche, pousse les chercheurs à présenter leurs résultats de la manière la plus impressionnante possible. Pour toucher les journaux à gros impact factor, ou pour décrocher un financement, il est de coutume d’insister sur les aspects surprenants et mystérieux de sa recherche. Une fois le pli pris, certains chercheurs gardent un ton inutilement grandiloquent et mystique avec le grand public. Il suffit d’en être conscient pour ne pas se faire avoir.

John S. Bell (IOP)

Il me semble que comme souvent, on peut s’inspirer des réflexions du physicien irlandais John S. Bell. Confronté à l’extrême bizarrerie de la mécanique quantique, Bell offre un critère intéressant pour départager les différentes interprétations des résultats expérimentaux : le romantisme. Le concept a évidemment ici un sens très différent de son acceptation usuelle en littérature. Pour Bell, le romantisme d’une théorie est ce que cette dernière contient de mystique ou de contre intuitif et qui n’est pas rendu absolument nécessaire par l’ensemble des faits que l’on cherche à modéliser. Pour Bell, on doit minimiser ce romantisme au maximum afin d’être certain que le caractère révolutionnaire que l’on attribue à tel ou tel phénomène n’est pas un pur artefact de sa modélisation. La transparence m’oblige d’ores et déjà à préciser qu’en mécanique quantique, ce choix ne fait pas toujours l’unanimité : de nombreux physiciens privilégient des interprétations baroques quand cela simplifie leurs calculs ou leur fournit des intuition boosts. Je pense qu’il s’agit néanmoins d’une assez bonne leçon à la fois pour ceux qui cherchent à construire de nouvelles théories physiques et pour ceux qui les vulgarisent. Privilégier toujours l’interprétation la plus terre à terre de résultats est probablement moins vendeur que d’enchaîner les tours de magie. Cette ascèse est en revanche indubitablement plus émancipatrice pour le public dont on a momentanément l’attention.

Le problème de la neutralité

En imaginant que la confiance du public lui est acquise et qu’il n’a pas de problème d’ego, le vulgarisateur peut tomber dans un dernier travers : perdre de vue son objectif et exploiter son auditoire plutôt que de lui enseigner quelque chose. Le troisième et ultime défaut est ainsi de se servir du public pour court-circuiter l’évaluation par les pairs et fourguer sa camelote spéculative en tout impunité. Je ne parle ici des purs crackpots hors de tout système académique et qui en deux équations prétendent faire tomber Einstein. Ces derniers posent un problème réel  mais essentiellement distinct car ils n’ont aucune rétroaction sur la communauté scientifique. Je veux plutôt parler de la tentation pour des physiciens légitimes de vulgarisent leurs thèses au grand public avant leur validation, donnant ainsi en retour l’impression à leurs pairs que les dites thèses sont déjà largement acceptées.

Aux États-Unis, où l’état de la vulgarisation scientifique est probablement meilleur qu’en France, la prise en otage du public est en contrepartie plus courante. L’exemple historique le plus significatif est sans doute celui de la théorie des cordes qui a été vulgarisée bien avant d’être validée expérimentalement (elle ne l’est toujours pas). Un nombre incalculable d’émissions de télévision a été consacré à la théorie, généralement avec un Brian Greene en transe expliquant comment les cordes changent profondément notre compréhension du monde. Les jeunes ados intéressés par la physique veulent maintenant qu’on leur parle des dimensions cachées, des espaces de Calabi-Yau et de l’infinie zoologie de concepts qui a été développée dans ce champ de recherche. Au fond le problème n’est même pas de savoir si la théorie des cordes est effectivement la théorie ultime de l’univers (disons pour être diplomatique que pour la plupart des théoriciens, elle a changé d’objectif). Mais simplement, et je prends ici le risque d’une légère exagération : il est impossible pour le public d’apprendre quoi que ce soit d’utile ou de raisonnablement profond sur ce sujet.

Un exemple de vidéo promotionnelle de Greene sur la théorie de cordes

Un autre exemple récent qui me semble illustratif de cette exploitation est l’importante couverture médiatique d’une prépublication récente du physicien néerlandais Erik Verlinde. Verlinde est un physicien de premier plan, pris au sérieux à raison. Sa dernière prépublication propose une nouvelle approche de la gravitation supposée résoudre certains problèmes actuellement rencontrés en cosmologie. L’université d’Amsterdam a dégainé un communiqué de presse avec une petite vidéo introductive de Verlinde, l’Independent a relayé l’information ce qui a contraint la journaliste scientifique Natalie Wolchover (par ailleurs excellente) à écrire un article sur le sujet pour le magazine Quanta. Sabine Hossenfelder a embrayé en tentant une présentation des idées de Verlinde sur son blog populaire Backreaction. Là où tout ça est gênant, c’est que la prépublication de Verlinde n’a même pas encore passé le filtre du comité de lecture. Pour avoir lu le papier en diagonale, je pense qu’il aurait été préférable de se calmer : le contenu est extrêmement spéculatif, les affirmations principales sont justifiées presque uniquement par des arguments heuristiques. On a évidemment le droit d’écrire des articles spéculatifs, il faut bien commencer quelque part quand on propose une nouvelle théorie. En revanche, on doit dans ce cas être prudent et modéré dans les affirmations que l’on fait sur la base de ces spéculations, en particulier lorsque l’on cherche à en parler au public. J’ai conscience de mélanger ici vulgarisation et communication scientifique, mais comme une grande partie de l’information à laquelle le public est exposé prend cette seconde forme, elle n’est pas à négliger.

extrait de la vidéo où Verlinde explique sa théorie révolutionnaire

L’exemple de la dualité onde-corpuscule

Je passe maintenant à un concept qui est particulièrement difficile à vulgariser : la dualité onde corpuscule. Il va me permettre d’évoquer une méthode de vulgarisation qui n’est pas directement problématique mais qui peut être dangereuse. Mais d’abord qu’est ce que la dualité onde-corpuscule ? C’est typiquement le sujet sur lequel on peut lancer une centaine de formules qui “claquent” et qui n’ont essentiellement aucun sens comme “la lumière est à la fois une onde et une particule”. Après quelques gesticulations et pour donner une intuition de ce que cela peut bien vouloir dire on fait parfois appel au dessin suivant :

Évidemment c’est sympa et bien vu, mais au fond je ne sais pas bien ce qu’on peut en tirer. Les physiciens ont ils accès à un monde d’une subtilité supérieure dans lequel la combinaison de propriétés incompatibles est miraculeusement possible ? C’est à ce stade que je pense qu’il faut être honnête : aucun physicien ne sait ce que veut dire être à la fois une onde et une particule. La fameuse dualité onde-corpuscule apparaît quand on étudie des problèmes mettant en jeu la lumière à l’aide de la mécanique quantique. La mécanique quantique est une théorie instrumentaliste, c’est à dire qu’elle ne parle pas du réel mais exclusivement de la statistique des résultats de mesure que l’on fait. C’est une sorte de méthode de prédiction mais qui ne dit pas ce qui se passe en coulisses pour produire les résultats que l’on observe. Suivant la situation, les prédictions que fait la mécanique quantique pour la lumière ressemblent aux prédictions que l’on ferait usuellement pour des ondes ou au contraire pour des corpuscules. Mais la mécanique quantique ne dit rien de la nature même de la lumière. La réponse honnête est donc que l’on ne sait pas ce qu’est la lumière mais que dans ses manifestations, on retrouve tantôt des propriétés typiques des ondes, tantôt des propriétés typiques des corpuscules. La dualité n’est pas ontologique (au niveau de ce qui est) mais simplement dans les observations. On ne comprend pas plus que ça.

Maintenant il n’est pas interdit d’imaginer vouloir aller plus loin et raffiner la question. Existe-t-il des théories, éventuellement spéculatives, qui proposent de regarder derrière le voile et se prononcent sur la nature de la lumière tout en étant compatibles avec la mécanique quantique ? Oui, et alors on a plusieurs ontologies possibles. Dans une première proposition, la théorie de de Broglie-Bohm, il y a simplement les deux objets à la fois : une onde et une particule qui évoluent de manière jointe (pour les experts, je passe sur le fait que dans le cas du photon, définir la trajectoire de la particule est difficile). Dans une autre proposition, les “modèles de collapse”, il n’y a qu’une onde qui se localise parfois dans un espace si petit qu’elle ressemble à une particule. L’explication plus élaborée de la dualité onde-corpuscule est donc qu’avec la théorie standard on n’a aucune idée mais qu’il existe des théories alternatives qui font des propositions contradictoires (et rien n’empêche de choisir celle qu’on préfère tant qu’aucune des deux théorie n’a été falsifiée).

Je me trompe peut-être, mais il me semble que cette réponse honnête est rarement faite. En général, on file les métaphores à l’infini, on en appelle à la poésie, prend des airs inspirés pour insister sur la beauté, le mystère de la chose; comme des exégètes devant la trinité. Je ne critique pas, je l’ai fait comme tout le monde. Je pense que lorsque l’on cherche à expliquer un sujet de manière simple et honnête les métaphores sont parfois dangereuses car on donne l’impression que la compréhension n’est accessible que par une forme de méditation ou de transcendance. On a d’autant plus tendance à jouer cette carte par complaisance lorsqu’on est face à un public à la fibre littéraire mais c’est encore une fois une erreur. Il est méprisant de penser que l’on ne peut parler de science à des gens dont la formation a été principalement dans les humanités qu’en la recouvrant d’un vernis littéraire ou pseudo-poétique. C’est le même type de mépris (inversé) qui fait que l’on demande aux candidats à l’épreuve de français-philosophie des concours scientifiques d’écrire leur dissertation “scientifiquement” sur des sujets comme “penser l’Histoire” ou “les énigmes du moi” où une telle froideur est ridicule. Je vais y revenir.

Retour en France

On peut maintenant quitter l’abstraction et s’intéresser momentanément à la situation française et à ses spécificités. En France, l’univers des vulgarisateurs populaires est assez pauvre. Passons rapidement sur les frères Bogdanov qui sont simplement des charlatans. Ils ont à leur actif un historique infini d’entourloupes qui, bien que passionnant, est trop long pour être raconté ici. Ensuite, en terme de livres vendus, je crois qu’on arrive immédiatement à Étienne Klein dont j’ai dit ce que je pensais : Klein ne dit pas de conneries, au pire se la raconte-t-il un peu trop. À mon avis, il ne faut pas rechercher excessivement la pureté et la popularité de Klein ne me dérange pas. Klein avait aussi le mérite, mais cela va peut-être changer, de protéger le public du full scale postmodern bullshit d’un autre physicien populaire.

Je n’en veux pas personnellement à Aurélien Barrau : il semble sincère dans sa passion pour la french theory et l’obscurité érigée en vertu. Il est aussi un physicien professionnel et actif dont je n’ai aucune raison de douter que les résultats soient sérieux. Mais je dois avouer que je serais fortement inquiet si, aidé des médias, il devenait la figure populaire de la physique en France. Je ne veux pas m’étendre indéfiniment sur ce qui fait que le personnage m’inquiète (on peut lire l’analyse serrée et édifiante de l’oeuvre “grand public” de Barrau par Vincent Debierre sur le carnet Zilsel). Pour résumer, avec Barrau, on se vautre allègrement dans l’obscurité romantique; on n’a plus que de la mousse. Tous les défauts précédemment évoqués sont présents en concentré, mais comme si ça n’était pas suffisant, Barrau mélange à cette écume ce que la philosophie française a eu de moins glorieux. Là ou Barrau est dangereux, c’est qu’il raconte aux journalistes et à l’élite littéraire ce qu’ils veulent entendre : que la science et la littérature ne sont pas si différentes et que la seconde donne une sorte d’accès privilégié à la première. Et en brossant les médias dans le sens du poil, Barrau s’offre un accès privilégié au grand public. De manière intéressante, les passages plagiés par Klein et qui faisaient sa patte avaient un objectif similaire : servir de sucre littéraire ou poétique pour faire avaler une science (supposément amère) à un public récalcitrant.

Extrait d’une interview d’Aurélien Barrau dans Ciel et Espace, crédit : un tweet d’Aurélien Barrau

Évidemment, je ne veux surtout pas me faire l’avocat d’un style froid et mécanique lorsqu’il s’agit de vulgarisation : si la forme peut servir le fond, tant mieux. Mais il faut garder à l’esprit l’avertissement précédent sur l’usage abusif des métaphores. Quand le discours que l’on tient devient trop éthéré, on prépare le terrain aux vrais charlatans et aux marchands de bullshit New-Age comme Deepak Choprah. On ne peut pas reprocher au public de ne pas savoir distinguer la science du charlatanisme quand les deux sont vendus dans le même langage.

À l’École Normale Supérieure

Jusqu’à maintenant, j’ai pu donner l’impression de jouer le rôle de redresseur de tort. Ça n’est pas mon objectif. Je n’ai pas eu à chercher loin les possibles travers précédemment évoqués : je ne fais au fond que résumer ce par quoi je suis passé en apprenti vulgarisateur. Ma modeste expérience dans le domaine vient de l’organisation du cours de Physique pour tous à l’ENS (un cours de physique pour les élèves non scientifiques). Il s’agit d’une frange certes un peu élitiste de la vulgarisation mais qui était à mon avis importante. Le système français cloisonne assez tôt et des élèves exceptionnellement intelligents se retrouvent à ne quasiment plus faire de sciences à partir de la classe de première. Ces élèves, s’ils ont eu la chance de passer par la rue d’Ulm, diffusent ensuite dans l’enseignement supérieur mais aussi dans les hautes sphères de l’État et les médias. Cette formation sans science ne peut ensuite qu’engendrer au mieux l’indifférence au pire l’hostilité à l’égard de tous les sujets vaguement techniques. Bref, il s’agissait dans notre cas d’essayer d’enseigner un peu de physique à des élèves brillants afin d’éviter que l’humanité ne les perde à l’alcool, au programme sociologique fort, ou à Alain Badiou.

Les premières années de Physique pour tous donnaient probablement excessivement dans la “hype facile” et les métaphores moisies et nous n’étions sauvés de l’utilisation abusive de l’argument d’autorité que par notre incompétence manifeste. Reste que nous (avec Antoine Bourget, Irénée Frérot, Pierre Ronceray et d’autres qui m’ont aidé plus ponctuellement) avons progressé les années suivantes et que le séminaire a eu un succès modeste mais décent. Rien n’a été magique, il a fallu travailler des dizaines d’heures pour construire des cours adaptés au public, et parfois se planter tristement en sortant un truc imbitable après des après-midis entières de réflexion. La vulgarisation, c’est difficile et il faut travailler beaucoup.

Nous avions évidemment face à nous des élèves particuliers, qui avaient une réelle volonté d’apprendre des choses, de comprendre le monde qui les entoure. Comme beaucoup, ils souffraient de cette spécialisation précoce et de l’impossibilité de reprendre la science à l’ENS dans le circuit classique. L’ENS ne favorise en effet la pluridisciplinarité que sur le papier pour les littéraires. Les élèves peuvent assister aux cours scientifiques “standards” : formidable. Simplement dès la première séance, on diagonalise des matrices symétriques et calcule des transformées de Fourier, de la magie noire pour les élèves qui se sont arrêtés aux pourcentages.

Je rêverais d’un modèle de Physique pour tous extensible hors des murs de l’ENS (j’espère en tout cas que nos successeurs maintiendront le séminaire en vie). Ce serait très certainement irréaliste et le public idéal de la rue d’Ulm n’est probablement pas représentatif du reste de la France. Peut-être peut-on néanmoins étendre l’esprit de ce genre de vulgarisation ? Que des jeunes chercheurs/professeurs produisent du contenu adapté et se donnent un peu de mal pour améliorer la culture scientifique en France ? Il y a déjà quelques exemples prometteurs avec, par exemple, David Louapre en physique et eljjdx en mathématiques. Ces deux auteurs travaillent manifestement beaucoup leurs explications et, pour ce que j’en ai lu, ne tombent dans aucun des trois pièges précédemment évoqués. Ne consommant moi même que peu de vulgarisation en physique, je suis sûr de passer à côté d’un nombre important d’initiatives intéressantes de ce type mais je suis persuadé qu’il y en a d’autres à promouvoir (ou, à défaut, à créer).

La culture scientifique moyenne des français est désastreuse. Mais si le succès des charlatans montre une chose c’est bien qu’il y a une réelle demande pour de la vulgarisation et de l’information scientifique. Les chercheurs, jeunes et vieux, ont leur responsabilité dans le manque cruel de matériel de bonne qualité qui pousse les gens à lire les idiots en combinaisons argentées. Il n’est jamais trop tard pour réagir.

Je remercie Antoine Bourget pour sa relecture de ce billet écrit au fil du clavier et pour ses suggestions.

I have just arrived at the ICTS in Bangalore for a three week school/conference on “fundamental problems in quantum physics“. The program looks quite promising with a first week on basic theoretical introductions (where I will admittedly not learn much, except for the course on Trace Dynamics by Tejinder Singh), a second week on experiments (where I will learn a lot, being a rookie on the matter) and a last week of shorter advanced talks. As usual, I will have a model to sell but I am principally interested in having a better view of the field and of what people are doing. I also have a few “foundational” projects I want to write drafts about and I hope the ICTS environment, where such a work is seen favorably, will gently motivate me.

A first view of the brand new ICTS campus

The whole thing takes place on the campus of the International Center for Theoretical Science (ICTS) which is impressively modern and clean. It is a small pocket of calm located just  at the boundary of the busy city of Bangalore and an Indian heaven for theoretical and experimental physicists.

The campus is only “98% complete” and still lacks a few trees.

I hope I will still find time to go out of the ICTS fortress and visit the surroundings (while avoiding encounters with snakes if possible). As with the Detlef farewell, I will try to summarize the most significant or interesting points discussed in upcoming posts.