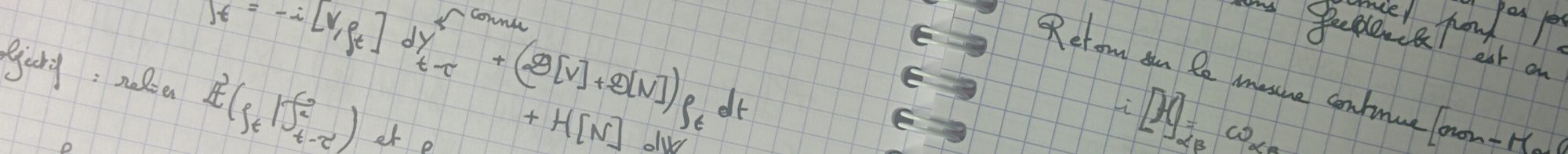J’ai écrit un petit article dans Pour la Science sur les réseaux de tenseurs et le lien avec la suprématie quantique. J’ai essayé d’adopter un angle un peu différent en ne mentionnant la bataille sur les problèmes de suprématie pure qu’en incipit.

De mon point de vue, l’intérêt principal des réseaux de tenseurs comme des ordinateurs quantiques est de résoudre le problème à N corps quantique dans des cas difficiles. Je rappelle ainsi dans cet article principalement ce qu’est ce problème, et les stratégies utilisées pour le résoudre. La conclusion, qui rejoint par exemple l’avis de Garnett Chan que j’aurais dû citer, c’est que pour le problème à N corps, il n’est pas évident que les ordinateurs quantiques seront forcément la meilleure méthode pour les instances utiles. C’est possible, mais ça n’est pas évident, et les algorithmes classiques pourront résister plus longtemps pour les problèmes utiles que pour les problèmes de suprématie pure.

Évidemment, pour les rares applications classiques établies comme l’algorithme de Shor, l’avantage de l’ordinateur quantique est asymptotiquement clair. De ce point de vue, je ne suis pas du tout un sceptique de l’avantage quantique. Je trouverais fascinant pour l’humanité qu’une énorme machine factorise des gros nombres en utilisant les lois bizarres de la physique fondamentale.

Mais si l’avantage quantique est restreint à quelques problèmes de théorie des nombres (d’intérêt pratique à mon avis bien moindre que le problème à N corps), alors l’impact pour la société sera inférieur à ce que certains prévoient. Je pense que même si on travaille dans une équipe qui cherche ultimement à améliorer le hardware d’ordinateurs quantiques, ce qui est mon cas avec Quantic (joint venture Inria, ENS, Mines), on doit rester lucide sur ce point.

note I : au moins temporairement, l’article est lisible gratuitement sur la preview du magazine de septembre – mais n’hésitez pas à l’acheter pour soutenir le journal (ça ne change rien à ce que je touche pour la pige !)

note II : dans la courte notice biographique, l’article ne mentionne que l’institution qui paie généreusement mon salaire, et à laquelle j’enseigne : le Centre Automatique et Systèmes de Mines Paris – PSL. Mea culpa. Il aurait dû mentionner aussi l’institution qui m’héberge (ainsi que mon groupe) dans d’exceptionnelles conditions matérielles tout en me fournissant de brillants collègues : Inria Paris. À ces deux honorables institutions s’ajoute le laboratoire de physique de l’ENS-PSL, qui fait lui aussi partie de l’équipe projet Quantic, et en héberge la partie expérimentale. J’y suis aussi mécaniquement affilié. Le laboratoire de Physique de l’ENS-PSL étant une unité mixte de recherche avec le CNRS, il faut donc aussi le remercier. Si l’article vous déplaît, vous avez ainsi un large choix d’institutions auprès desquelles vous plaindre !

J’ai donné pour la deuxième année consécutive le TD du cours d’optimisation convexe de première année des Mines Paris. J’ai écrit quelques notes pour aider les étudiants à visualiser les théorèmes du cours. Elles peuvent peut-être en aider d’autres… À lire en restant vigilant, car c’est un domaine où je ne suis qu’un amateur (dans les deux sens du terme : de celui qui débute, et de celui qui apprécie — double sens auquel m’a initié Denis Bernard, mon directeur de thèse) . J’ai pas mal utilisé les méthodes d’optimisation (surtout dans le cas différentiable et sans contrainte) pour ma recherche, mais je n’ai appris la théorie (et les cas plus fins, par exemple non différentiables) essentiellement qu’avec ces TD. Pour ceux qui veulent aller plus loin que ces notes ultra basiques, le mieux est de jeter un œil à Numerical Optimization de Nocedal et Wright.

I put a first postdoc offer on Inspire a few days ago. I am looking for smart independent people, who are ideally willing to push the use of tensor network methods in quantum field theory.

The application has a very close deadline in the advertisement, so that I can make offers to candidates in sync with the standard high energy theory postdoc cycle (to which I was only partly familiar with a few days ago). If you are interested and cannot assemble all the documents by the deadline, feel free to contact me and to apply still. If you really arrive too late, I will open another postdoc position later, still funded by the ERC.

It is now official: the ERC awarded me generous research funding to work on the intersection of tensor networks and quantum field theory (see e.g. here). The proposal that got me the money is here and, as far as I am concerned, it is public (I will be happy if you can solve the open problems faster than my collaborators and I). Some formal job openings will follow but you can already check the “working with me” section.

Soon, I will have to work. But now I thank the people who helped me. Thanks to those who proofread my proposal and pushed me to apply (in particular Pierre Rouchon). Thanks also to Jean-Pierre Banatre who helped me prepare for the interview. Thanks to Mathieu Reboul at Armines who took care of the admin part and allowed me to focus on the science. Thanks, to the UK for leaving the ERC, which apparently allowed my project to go from “recommended for funding” to “funded“. Thanks finally to randomness — whether it comes from the splitting of many worlds, the collapse of the wave function, or the last digits of the Bohmian positions at the beginning of time — it certainly helped me.

I am at the Erwin Schrödinger Institute in Vienna for 1 more week, where I get a perfusion of tensor networks straight into my veins. There, I unsurprisingly talked about my recent work on continuous matrix product states. The blackboard talk was recorded, but sadly I wrote a little too small so I have to squint to read the equations. It is adapted to an audience knowing tensor networks very well, but quantum field theory slightly less.

To have more things to discuss at the breaks, I put on arxiv the results of my exploration of the ground state of the Sinh-Gordon model with relativistic continuous matrix product state. This is not a final version (some references are missing, and I will likely update the discussion), but I had to put it online at some point. I spent quite a lot of time optimizing the numerics but at the end still couldn’t fully settle the situation of the model near its self dual point. I still think the data is interesting nonetheless: it is obtained in the thermodynamic limit, and is fairly precise for moderate coupling. I hope it will also push people to develop better contraction routines, as ramping up the bond dimension could be enough to clarify the matter (at least numerically, before mathematical physicists and mathematicians nail it).

update: this position is now filled, but there will be new PhD and postdoc offerings very soon, on similar topics.

———–

I am now looking for a PhD student to work with me, starting next year (December 2022 at the latest). I have the money, I just need a smart person. The ideal topic, described in more detail in the offer below, would be tensor networks and their use in non-perturbative quantum field theory. However, I am open to inquiries on any other of my past subjects, so if there is something you are interested in, feel free to contact me!

The best is to start with an internship, to get a feel for the subject. This is why it is important to contact me asap if you’re interested, even before the offer is formally advertised on the website of the école doctorale.

1- Since October 4th, I am back in Paris with a position at Mines Paristech, which is a French “grande école” part of Paris Science et Lettres (PSL). I am also a member of the Quantic group, which is a joint venture with Inria and École Normale Supérieure exploring superconducting circuits for quantum information processing (theoretically and experimentally). I am very happy about this move back to Paris after 5 great years in Munich where I learned immensely and became more of an “adult” theoretical physicist. In Paris I will keep an interest in my old subjects: quantum field theory with variational methods, many body physics, quantum foundations (and others..). But I will try to develop tighter connection between state compression methods (tensor networks) and what is done in the group especially with cat qubits and error correction. For all these subjects, I will probably have some money soon from various sources. Students interested in any of these themes (even the exotic stuff) should feel free to contact me in advance to discuss possible PhDs or internships.

2- I gave a rather conceptual talk on collapse models at the Quantum Boundaries workshop. The talk was recorded:

3- For those who are in Paris, I will speak at Foundation 2020 (which was delayed because of covid) on Thursday October 28th. I will present our latest results with Howard Wiseman on the equivalence between non-Markovian collapse models and Bohmian theories (this preprint).

For the European Tensor Network school 2021 at ICCUB in Barcelona, I started to write some lecture notes on continuous tensor network states. So far they cover only continuous matrix product states, which is a pretty stabilized subject. I tried to make them very detailed about the computations which can be scary for beginners. I plan (or rather hope) to extend the notes to include more recent developments like relativistic extensions in 1 space dimension, and non-relativistic extensions in 2 space dimensions and more.

J’ai discuté il y a quelques jours avec Vincent Debierre (du podcast Libaca) du problème de l’unification (ou de la jonction) entre modèle standard et gravité. J’ai surtout essayé de clarifier la logique : qu’est-ce qu’on cherche à faire, qu’est-ce qui est a priori possible et qu’est-ce qui ne l’est pas ?

Pour ceux qui peuvent passer outre ma grammaire floue et mon élocution un peu non-linéaire, c’est un moyen d’avoir une idée de ce domaine d’un point de vue peut-être hétérodoxe. Je suis aussi preneur de commentaires éventuellement critiques sur la présentation du problème, car je ne suis évidemment pas sans biais.

À la fin, je mentionne aussi les réseaux de tenseurs. C’est une nouvelle méthode pour résoudre numériquement des modèles existants difficiles (et non un nouveau modèle de la nature) qui est assez à la mode et qui m’occupe aujourd’hui davantage que la gravité. Je suis curieux de savoir si la philosophie en est compréhensible en quelques phrases.

Today I put online a major update of my pair of papers on the variational method for quantum field theory (short here, long here). The idea is still to use the same class of variational wave functions (relativistic continuous matrix product states) to find the ground state of (so far bosonic) quantum field theories in 1+1 dimensions. The novelty comes from the algorithm I now use to compute expectation values, that has a cost only proportional to where is the bond dimension. Using backpropagation techniques, the cost of computing the gradient of observables with respect to the parameters is also only . This is basically the same asymptotic scaling as standard continuous matrix product states.

Previously, the method was a nice theoretical advance as it worked without any cutoff, but it was not numerically competitive compared to bruteforce discretization + standard tensor methods (at least not competitive for most observables insensitive to the UV). With the new algorithm with improved scaling, I can go fairly easily from to , which gives relative error for the renormalized energy density at a coupling of order 1. Crucially, the error really seems to decrease exponentially as a function of the bond dimension, and thus with only a slightly higher numerical effort (say 100 times more) one could probably get close to machine precision. Already at relative error for the renormalized energy density, that is a quantity where the leading lattice contribution has been subtracted, I doubt methods relying on a discretization can compete. This makes me a bit more confident that methods working directly in the continuum are a promising way forward even if only for numerics.

Now, let me go a bit more into the technicalities. Computing expectation values of local functions of the field with such a low cost seems difficult at first because the ansatz is not written in terms of local functions of . Naively this should at the very least square the cost to . The main idea to obtain the cheap scaling is to realize that the expectation value of vertex operators, i.e. operators of the form , can be computed by solving an ordinary differential equation (ODE) where the generator has a cost . Basically, computing vertex operators for relativistic CMPS is as expensive as computing field expectation values for standard non-translation-invariant CMPS. To solve this ODE, one can use powerful method with extremely quickly decaying errors as a function of the discretization step (e.g. very high order Runge-Kutta). So vertex operators are, in fact cheap. But local powers of the field are merely differentials of vertex operators, and thus can be computed as well for the same cost. Finally, to get the gradient, one can differentiate through the ODE with backpropagation, and obtain the result for only twice the cost. This allows the full variational optimization for all well-defined bosonic Hamiltonians with polynomial and exponential potentials.